Menerapkan Statistik Deskriptif dan Statistik Inferensial di Python
- Cornellius Yudha Wijaya
- 25 Jul 2024
- 8 menit membaca
Statistik adalah bidang yang mencakup aktivitas pengumpulan data, analisis data, hingga interpretasi data. Ini adalah bidang studi yang membantu pihak terkait untuk membuat keputusan ketika menghadapi ketidakpastian.
Dua cabang utama dalam bidang statistik adalah statistik deskriptif dan statistik inferensial.
Statistik deskriptif adalah cabang yang terkait dengan peringkasan data menggunakan berbagai cara, seperti statistik ringkasan (summary statistics), visualisasi, dan tabel. Sedangkan statistik inferensial lebih tentang generalisasi populasi berdasarkan sampel data.
Artikel ini akan membahas beberapa konsep penting dalam statistik deskriptif dan statistik inferensial menggunakan contoh Python. Mari kita mulai.
Statistik Deskriptif
Seperti yang telah saya sebutkan sebelumnya, statistik deskriptif berfokus pada ringkasan data (data summarization). Ini adalah ilmu untuk memproses data mentah menjadi informasi yang bermakna. Statistik deskriptif dapat dilakukan dengan grafik, tabel, atau summary statistics (statistik ringkasan). Namun, summary statistics adalah cara paling populer untuk melakukan statistik deskriptif, jadi kita akan fokus pada hal ini.
Untuk contoh kita, kita akan menggunakan contoh dataset berikut.
import pandas as pd
import numpy as np
import seaborn as sns
tips = sns.load_dataset('tips')
tips.head()Dengan data ini, kita akan mengeksplorasi statistik deskriptif. Dalam summary statistics, ada dua yang paling sering digunakan: Ukuran Pemusatan (Measures of Central Tendency) dan Ukuran Penyebaran (Measures of Spread).
Ukuran Pemusatan
Ukuran Pemusatan adalah pusat distribusi data atau dataset. Ukuran pemusatan adalah aktivitas untuk memperoleh atau menggambarkan distribusi pusat dari data kita. Ukuran pemusatan akan memberikan nilai tunggal yang mendefinisikan posisi pusat data.
Dalam ukuran pemusatan, ada tiga pengukuran populer:
Mean
Mean atau rata-rata adalah metode untuk menghasilkan output nilai tunggal yang mewakili nilai yang paling umum dari data kita. Namun, mean tidak selalu merupakan nilai yang diamati dalam data kita.
Untuk menghitung rata-rata, kita bisa menjumlahkan semua nilai yang ada dalam data dan kemudian membaginya dengan jumlah nilai tersebut. Cara menghitung rata-rata dapat dituliskan dengan persamaan berikut:
Pada Python, kita dapat menghitung mean data dengan kode berikut.
round(tips['tip'].mean(), 3)2.998Menggunakan atribut pandas series, kita dapat memperoleh mean data. Kita juga membulatkan data untuk memudahkan pembacaan data.
Mean memiliki kelemahan sebagai ukuran pemusatan karena sangat dipengaruhi oleh outlier, yang dapat menggeser summary statistic dan tidak mewakili situasi sebenarnya. Dalam kasus yang skewed, kita dapat menggunakan median.
2. Median
Median adalah nilai tunggal yang ditempatkan di tengah data jika kita mengurutkannya, yang mewakili posisi tengah data (50%). Sebagai ukuran pemusatan, median lebih disukai ketika data skewed karena dapat mewakili pusat data, karena nilai outlier atau skewed tidak terlalu mempengaruhinya.
Median dihitung dengan mengatur semua nilai data dalam urutan menaik (dari terkecil ke terbesar) dan menemukan nilai tengahnya. Median adalah nilai tengah untuk jumlah data yang ganjil, tetapi median adalah rata-rata dari dua nilai tengah untuk jumlah data yang genap.
Kita dapat menghitung Median dengan Python menggunakan kode berikut.
tips['tip'].median()2.93. Mode
Mode adalah nilai yang paling sering muncul dalam data. Data dapat memiliki satu mode (unimodal), beberapa mode (multimodal), atau tidak ada mode sama sekali (jika tidak ada nilai yang berulang).
Mode biasanya digunakan untuk data kategorikal tetapi juga dapat digunakan dalam data numerik. Pada data kategorikal, kita hanya bisa menggunakan mode, karena data kategorikal tidak memiliki nilai numerik untuk menghitung mean dan median.
Kita dapat menghitung Mode data dengan kode berikut.
tips['day'].mode()Hasilnya adalah objek series dengan tipe nilai kategorikal. Nilai Sat adalah satu-satunya yang muncul karena itu adalah mode data.
Ukuran Penyebaran
Ukuran penyebaran (atau variabilitas, dispersi) adalah pengukuran untuk menggambarkan penyebaran nilai data. Pengukuran ini memberikan informasi tentang bagaimana nilai data kita bervariasi dalam dataset. Ini sering digunakan dengan ukuran pemusatan karena saling melengkapi informasi data secara keseluruhan.
Ukuran penyebaran juga membantu memahami seberapa baik output ukuran pemusatan kita. Misalnya, penyebaran data yang lebih tinggi mungkin menunjukkan deviasi yang signifikan antara data yang diamati, dan mean data mungkin tidak mewakili data dengan baik.
Berikut adalah berbagai ukuran penyebaran yang dapat digunakan.
1. Range
Range adalah selisih antara nilai terbesar (Max) dan nilai terkecil (Min) dari data. Ini adalah pengukuran paling sederhana karena informasinya hanya menggunakan dua aspek dari data.
Penggunaannya mungkin terbatas karena tidak banyak menceritakan tentang distribusi data, tetapi mungkin membantu asumsi kita jika kita memiliki ambang tertentu untuk digunakan pada data kita. Mari kita coba menghitung range data dengan Python.
tips['tip'].max() - tips['tip'].min()9.02. Variance
Variansi adalah pengukuran penyebaran yang menginformasikan penyebaran data berdasarkan mean data. Kita menghitung variansi dengan menguadratkan selisih masing-masing nilai dengan mean data dan membaginya dengan jumlah nilai data. Karena kita biasanya bekerja dengan sampel data dan bukan populasi, kita mengurangi jumlah nilai data dengan satu. Persamaan untuk variansi sampel ada dalam gambar di bawah ini.
Variansi dapat diinterpretasikan sebagai nilai yang menunjukkan seberapa jauh data tersebar dari mean dan satu sama lain. Variansi yang lebih tinggi berarti penyebaran data lebih luas. Namun, perhitungan variansi sensitif terhadap outlier karena kita menguadratkan deviasi skor dari mean; ini berarti kita memberikan lebih banyak bobot pada outlier.
Mari kita coba menghitung variansi data dengan Python.
round(tips['tip'].var(),3)1.914Variansi di atas mungkin menunjukkan variansi tinggi pada data, tetapi kita mungkin ingin menggunakan Standard Deviation untuk memiliki nilai aktual untuk pengukuran penyebaran data.
3. Standard Deviation
Standard deviation adalah cara paling umum untuk mengukur penyebaran data, dan ini dihitung dengan mengambil akar kuadrat dari variansi.
Perbedaan antara variansi dan standar deviasi adalah informasi yang diberikan nilai keduanya. Nilai variansi hanya menunjukkan seberapa jauh nilai kita tersebar dari mean, dan satuan variansi berbeda dari nilai asli karena kita menguadratkan nilai asli.
Namun, nilai standar deviasi adalah satuan yang sama dengan nilai data asli, yang berarti nilai standar deviasi dapat digunakan langsung untuk mengukur penyebaran data kita.
Mari kita coba menghitung Standard Deviation dengan kode berikut.
round(tips['tip'].std(),3)1.384Salah satu aplikasi paling umum dari standar deviasi adalah untuk memperkirakan interval data. Kita dapat memperkirakan interval data menggunakan aturan empiris atau aturan 68–95–99.7.
Aturan empiris menyatakan bahwa 68% data diperkirakan berada dalam mean data ± satu STD, 95% data berada dalam mean ± dua STD, dan 99.7% data berada dalam mean ± tiga STD. Di luar interval ini, dapat diasumsikan sebagai outlier.
4. Interquartile Range
Interquartile Range (IQR) adalah ukuran penyebaran yang dihitung menggunakan selisih antara kuartil pertama dan kuartil ketiga dari data. Kuartil adalah nilai yang membagi data menjadi empat bagian berbeda. Untuk lebih memahami, mari kita lihat gambar berikut.
Kuartil adalah nilai yang membagi data, bukan hasil pembagiannya. Kita dapat menggunakan kode berikut untuk menemukan nilai kuartil dan IQR.
q1, q3= np.percentile(tips['tip'], [25 ,75])
iqr = q3 - q1
print(f'Q1: {q1}\nQ3: {q3}\nIQR: {iqr}')Q1: 2.0
Q3: 3.5625
IQR: 1.5625Menggunakan fungsi numpy percentile, kita dapat memperoleh kuartil. Dengan mengurangkan kuartil ketiga dan kuartil pertama, kita mendapatkan IQR.
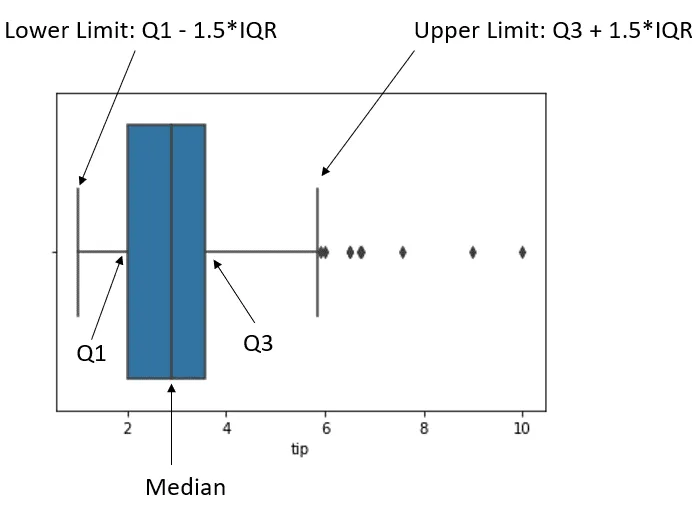
IQR dapat digunakan untuk mengidentifikasi outlier data dengan mengambil nilai IQR dan menghitung batas atas / batas bawah data. Rumus batas atas adalah Q3 + 1.5 IQR, sedangkan batas bawah adalah Q1–1.5 IQR. Setiap nilai yang melewati batas ini dianggap sebagai outlier.
Untuk lebih memahami, kita dapat menggunakan boxplot untuk memahami deteksi outlier IQR.
sns.boxplot(tips['tip'])Gambar di atas menunjukkan boxplot data dan posisi datanya. Titik hitam setelah batas atas adalah apa yang kita anggap sebagai outlier.
Statistik Inferensial
Statistik inferensial adalah cabang ilmu statistik yang berfokus pada pengambilan kesimpulan umum tentang keseluruhan populasi berdasarkan data sampel yang diambil dari populasi tersebut. Statistik inferensial digunakan karena seringkali tidak mungkin mendapatkan seluruh populasi data, dan kita perlu membuat inferensi dari sampel data.
Misalnya, kita ingin memahami pendapat masyarakat Indonesia tentang AI. Namun, jika kita mensurvei seluruh penduduk Indonesia, tentu akan memakan waktu yang sangat lama dan tidak efisien. Oleh karena itu, kita menggunakan sampel data yang mewakili populasi dan membuat inferensi tentang pendapat masyarakat Indonesia tentang AI.
Mari kita eksplorasi berbagai Statistik Inferensial yang dapat kita gunakan.
1. Standard Error
Standard error adalah pengukuran statistik inferensial untuk memperkirakan parameter populasi sebenarnya berdasarkan statistik sampel. Informasi standard error menunjukkan bagaimana statistik sampel akan bervariasi jika kita mengulangi percobaan dengan sampel data dari populasi yang sama.
Standard error of the mean (SEM) adalah jenis standard error yang paling umum digunakan karena menunjukkan seberapa baik mean akan mewakili populasi yang diberikan sampel data. Untuk menghitung SEM, kita akan menggunakan persamaan berikut.
Dalam statistik, standar error mean (SEM) dihitung menggunakan standar deviasi data sampel. Semakin tinggi jumlah sampel, semakin kecil standar error mean. Dengan kata lain, standar error mean yang lebih kecil menunjukkan sampel kita lebih baik dalam mewakili populasi data secara keseluruhan.
Untuk mendapatkan standard error of the mean, kita dapat menggunakan kode berikut.
from scipy.stats import sem
round(sem(tips['tip']),3)0.089Kita sering melaporkan SEM dengan mean data, di mana mean populasi sebenarnya diperkirakan berada dalam mean±SEM.
data_mean = round(tips['tip'].mean(),3)
data_sem = round(sem(tips['tip']),3)
print(f'The true population mean is estimated to fall within the range of {data_mean+data_sem} to {data_mean-data_sem}')The true population mean is estimated to fall within the range of 3.087 to 2.90900000000000032. Confidence Interval
Confidence interval juga digunakan untuk memperkirakan parameter populasi sebenarnya, tetapi ini memperkenalkan confidence level (tingkat kepercayaan). Confidence interval memperkirakan rentang parameter populasi sebenarnya dengan persentase kepercayaan tertentu.
Dalam statistik, kepercayaan dapat dijelaskan sebagai probabilitas. Misalnya, confidence interval dengan tingkat kepercayaan 90% berarti bahwa estimasi mean populasi sebenarnya akan berada dalam nilai atas dan bawah interval kepercayaantersebut 90 dari 100 kali. Confidence interval dihitung dengan rumus berikut.
Rumus di atas memiliki notasi yang familiar kecuali Z. Notasi Z adalah z-score yang diperoleh dengan menentukan tingkat kepercayaan (misalnya, 95%) dan menggunakan tabel z-critical value untuk menentukan z-score (1.96 untuk tingkat kepercayaan 95%). Selain itu, jika sampel kita kecil atau di bawah 30, kita seharusnya menggunakan tabel t-distribution.
Kita dapat menggunakan kode berikut untuk mendapatkan Confidence Interval dengan Python.
import scipy.stats as st
st.norm.interval(confidence=0.95, loc=data_mean, scale=data_sem)(2.8246682963727068, 3.171889080676473)Hasil di atas dapat diinterpretasikan bahwa mean populasi sebenarnya dari data kita berada dalam rentang 2.82 hingga 3.17 dengan tingkat kepercayaan 95%.
3. Hypothesis Testing
Hypothesis testing adalah metode dalam statistik inferensial untuk menarik kesimpulan dari sampel data tentang populasi. Estimasi populasi bisa berupa parameter populasi atau probabilitas.
Dalam Hypothesis testing, kita perlu memiliki asumsi yang disebut hipotesis nol (H0) dan hipotesis alternatif (Ha). Hipotesis nol dan hipotesis alternatif selalu berlawanan satu sama lain. Prosedur Hypothesis testing kemudian akan menggunakan sampel data untuk menentukan apakah hipotesis nol dapat ditolak atau kita gagal menolaknya (yang berarti kita menerima hipotesis alternatif).
Saat kita melakukan metode Hypothesis testing untuk melihat apakah hipotesis nol harus ditolak, kita perlu menentukan tingkat signifikansi (significance level). Tingkat signifikansi adalah probabilitas maksimum kesalahan tipe 1 (menolak H0 ketika H0 benar) yang diizinkan terjadi dalam tes. Biasanya, tingkat signifikansi adalah 0.05 atau 0.01.
Untuk menarik kesimpulan dari sampel, Hypothesis testing menggunakan P-value saat mengasumsikan hipotesis nol benar untuk mengukur seberapa mungkin hasil sampel terjadi. Ketika P-value lebih kecil dari tingkat signifikansi, kita menolak hipotesis nol; jika tidak, kita tidak dapat menolaknya.
Hypothesis testing adalah metode yang dapat dilakukan pada parameter populasi mana pun dan dapat dilakukan pada beberapa parameter juga. Misalnya, kode di bawah ini akan melakukan t-test pada dua populasi yang berbeda untuk melihat apakah data ini berbeda secara signifikan dari yang lain.
st.ttest_ind(tips[tips['sex'] == 'Male']['tip'], tips[tips['sex'] == 'Female']['tip'])Ttest_indResult(statistic=1.387859705421269, pvalue=0.16645623503456755)Dalam t-test, kita membandingkan rata-rata antara dua kelompok (uji berpasangan). Hipotesis nol untuk t-test adalah tidak ada perbedaan antara rata-rata dua kelompok, sedangkan hipotesis alternatif adalah bahwa ada perbedaan antara rata-rata dua kelompok.
Hasil t-test menunjukkan bahwa tip antara Male dan Female tidak berbeda secara signifikan karena P-value berada di atas tingkat signifikansi 0.05. Ini berarti kita gagal menolak hipotesis nol dan menyimpulkan bahwa tidak ada perbedaan antara rata-rata dua kelompok.
Tentu saja, tes di atas hanya contoh hypothesis testing sederhana. Ada banyak asumsi yang perlu kita ketahui saat melakukan hypothesis testing, dan ada banyak tes yang dapat kita lakukan untuk memenuhi kebutuhan kita.
Kesimpulan
Ada dua cabang utama bidang statistik yang perlu kita ketahui: statistik deskriptif dan statistik inferensial. Statistik deskriptif berkaitan dengan peringkasan data, sedangkan statistik inferensial menangani generalisasi data untuk membuat inferensi tentang populasi. Dalam artikel ini, kita telah membahas statistik deskriptif dan inferensial sambil memiliki contoh dengan kode Python.









留言